Piirilevyissä monet asiat voivat aiheuttaa EMI:tä. Esimerkiksi: radiotaajuus virrat, yhteisvirtajännitteet, maasilmukat, impedanssin epäsuhta ja magneettivuo. EMI:n hallitsemiseksi meidän on opittava nämä syyt vaihe vaiheelta ja nähtävä, miten ne vaikuttavat piirilevyyn. Voimme opiskella matematiikkaa sähkömagneettisesta teoriasta. Mutta se tie on pitkä ja vaikea. Useimmille insinööreille selkeät ja yksinkertaiset sanat ovat hyödyllisempiä. Tässä artikkelissa käsitellään: piirilevyn “sähkökenttien lähteitä”, Maxwellin yhtälöiden käyttöä ja magneettivuon minimoinnin ajatusta.
1. Sähkökentän lähteet
1.1 Sähköinen dipolimalli (ajassa muuttuva)
Sähkökenttien lähde mallinnetaan usein ajassa muuttuvana sähködipolina. Tämä on magneettilähteen päinvastainen ajatus. Sähköinen dipoli tarkoittaa kahta lähekkäistä, vastakkaista pistevarausta, jotka muuttuvat ajan myötä. Dipolin molemmissa päissä näkyy varauksen muutos. Tämä tapahtuu, koska virta kulkee dipolin koko pituudelta. Voit mallintaa sähköistä lähdettä ohjaamalla päättymätöntä antennia oskillaattorisignaalilla. Tämä piiri osoittaa, miten sähkölähde toimii. Sitä ei kuitenkaan voi selittää pelkästään matalataajuuspiirien ideoiden avulla.
Älä unohda, että signaalin etenemisnopeus ei ole ääretön. Nopeus riippuu ei-magneettisten materiaalien dielektrisyysvakiosta. Koska nopeus on äärellinen, piirissä esiintyy RF-virtaa. Ihmiset olettavat joskus, että johdossa on sama jännite joka pisteessä ja että piiri on aina tasapainossa joka hetki. Tämä ei pidä paikkaansa RF-virrassa.
1.2 Sähkömagneettisiin kenttiin vaikuttavat keskeiset tekijät
Sähköisen dipolin sähkömagneettinen kenttä riippuu neljästä asiasta:
- Virran amplitudi silmukassa: Kenttä on verrannollinen dipolissa kulkevaan virtaan.
- Dipolin napaisuus ja mittausantenni: Dipolin napaisuuden on vastattava mittauslaitteen antennin napaisuutta. Tämä on kuin magneettilähde.
- Dipolin koko: Kenttä on verrannollinen virtaelementin pituuteen. Viivan pituuden on kuitenkin oltava vain aallonpituuden osa. Mitä suurempi dipoli on, sitä pienempi on antennista mitattu taajuus. Tietyn koon tapauksessa antenni resonoi tietyllä taajuudella.
- Etäisyys: Sähkö- ja magneettikentät liittyvät toisiinsa. Niiden voimakkuus riippuu etäisyydestä. Kaukaisessa kentässä käyttäytyminen on kuin silmukan (magneettinen) lähde ja näet sähkömagneettisen tasoaallon. Lähellä pistemäistä lähdettä kentän riippuvuus etäisyydestä on voimakkaampi.
1.3 Lähikentän ja kaukokentän suhteet
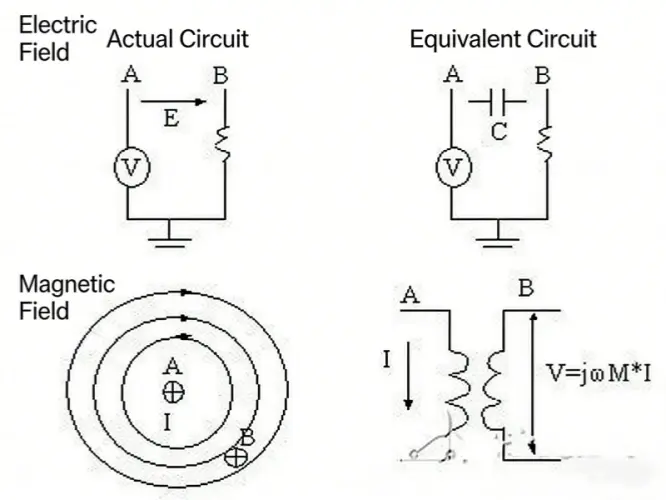
Lähikenttä ja kaukokenttä sisältävät sekä magneettisen että sähköisen osan. Kaikissa aalloissa yhdistyvät sähköiset ja magneettiset osat. Tämä sekoitus on Poyntingin vektori. Itse asiassa ei ole olemassa mitään puhdasta “sähköistä aaltoa” tai “magneettista aaltoa” yksinään. Voimme mitata tasoaaltoa, koska useiden aallonpituuksien päässä olevan pienen antennin kohdalla aaltorintama näyttää tasolta.
Pieni piirros voi auttaa. Siitä näkyisi aaltojen impedanssi ja etäisyys. Merkinnät olisivat seuraavat: aaltoimpedanssi; sähkökentän hallitsema alue, jossa E = 1/r ja H = 1/r²; tasoaalto, jossa Z = 377 Ω; asymptoottiviiva; todellinen muoto; magneettikentän hallitsema alue; siirtymäalue; lähikenttä H = 1/r³, E = 1/r²; kaukokenttä; vaaka-akseli 0,1, 0,5, 1,0, 5,0.
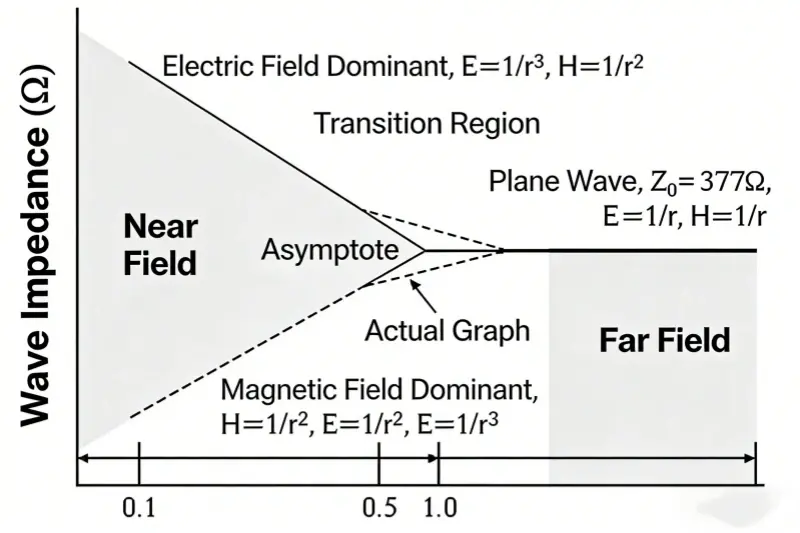
Tämä näkymä on antennin näkemä fyysinen “profiili”. Ajattele sitä kuin heittäisit kiven jokeen ja näkisit aaltoja. Kenttä säteilee pistelähteestä valon nopeudella. Nopeus riippuu dielektrisestä vakiosta. Sähkökentän yksikkö on V/m. Magneettikentän yksikkö on A/m. E:n ja H:n suhde on vapaan tilan impedanssi. Vapaassa tilassa olevan tasoaallon aaltoimpedanssi Z₀ on vakio. Se ei riipu etäisyydestä eikä pistemäisestä lähteestä. Vapaassa avaruudessa oleva tasoaalto sisältää energiaa watteina neliömetriä kohti.
1.4 Melukytkentä ja kertakomponenttimallit
Useimmissa Maxwellin yhtälöiden käyttökohteissa mallinnamme kohinan kytkeytymistä vastaavilla kiinteillä komponenteilla. Esimerkiksi: kahden johtimen välinen ajassa muuttuva sähkökenttä on kuin kondensaattori. Ajan suhteen muuttuva magneettikenttä kahden saman johtimen välillä on kuin keskinäinen induktanssi. Kuvassa voidaan esittää nämä kaksi kohinakytkentäpolkua.
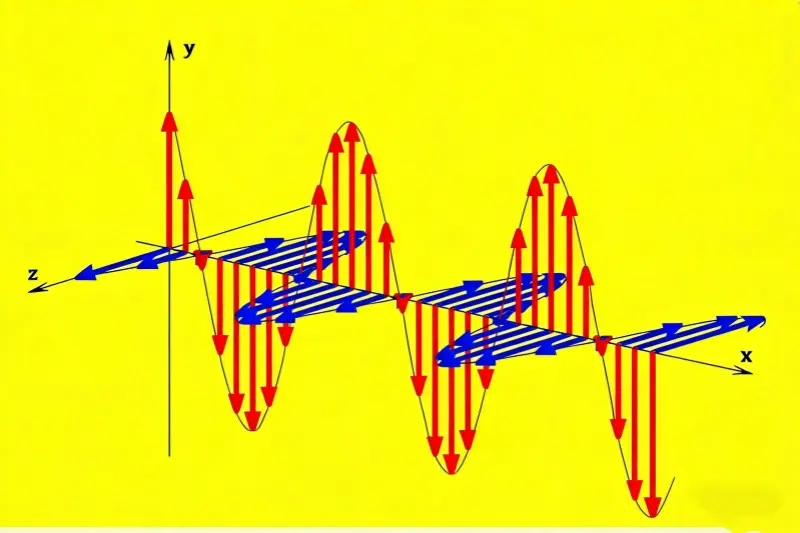
Jotta tällaiset kohinamallit olisivat oikeita, piirin on oltava pieni verrattuna signaalin aallonpituuteen. Jos tämä ei pidä paikkaansa, voimme silti käyttää EMC:n kuvaamiseen lumped component -malleja. Miksi? Koska Maxwellin yhtälöitä on vaikea soveltaa monissa todellisissa tapauksissa monimutkaisten rajojen vuoksi. Jos lumped-malli vaikuttaa suunnilleen oikealta, se on käyttökelpoinen. Useimmat erilliset komponentit käyttäytyvät yleensä luotettavasti.
Numeerinen malli ei aina näytä, miten kohina johtuu järjestelmän parametreista. Malli voi olla vastaus, mutta järjestelmäparametreja ei välttämättä tunneta, löydetä tai nähdä. Käytettävissä olevista malleista lumped-component-mallit ovat usein paras käytännön valinta.
1.5 Merkitys PCB-asettelulle
Miksi tutkimme tätä teoriaa PCB-asettelu? Yksinkertainen vastaus: meidän on tiedettävä, miten sähkömagneettiset kentät syntyvät. Sitten voimme vähentää RF-kenttiä piirilevyllä. Tämä tarkoittaa, että meidän on vähennettävä RF-virtoja piirissä. RF-virta liittyy signaalinjakeluverkkoon, ohitukseen ja kytkentään. RF-virta muodostaa lopulta harmonisia ja muuta digitaalista signaalisisältöä. Signaalinjakeluverkkojen on oltava mahdollisimman pieniä. Se vähentää RF-paluuvirtasilmukoiden pinta-alaa. Ohitus ja kytkentä liittyvät suuriin virtoihin, ja niiden on tapahduttava virranjakeluverkon kautta. Tehonjakeluverkossa on määritelmän mukaan suuria RF-paluusilmukka-alueita.
2. Maxwellin yhtälöiden soveltaminen
2.1 Maxwellin yhtälöiden yhdistäminen Ohmin lakiin
Esittelimme edellä Maxwellin perusajatukset. Mutta miten sovellamme tätä fysiikan ja laskennan tietämystä piirilevyn EMC:hen? Meidän on yksinkertaistettava Maxwellin yhtälöitä, jotta voimme käyttää niitä piirilevyn jälkiä varten. Voimme yhdistää Maxwellin yhtälöt Ohmin lakiin.
Ohmin laki aika-alueella:
V = I × R.
Ohmin laki taajuusalueella:
V_rf = I_rf × Z.
Tässä V on jännite, I on virta, R on resistanssi ja Z on impedanssi (Z = R + jX). rf tarkoittaa radiotaajuista energiaa. Jos RF-virta kulkee piirilevyn jäljessä, jolla on kiinteä impedanssi, syntyy RF-jännite. RF-jännite on verrannollinen RF-virtaan. Huomautus: aaltomallissa R korvataan Z:llä. Z on kompleksinen. Sillä on resistanssi (reaalinen) ja reaktanssi (imaginaarinen).
2.2 Johdinten/piirilevyjen impedanssikaavat
Impedanssi voidaan kirjoittaa monella eri tavalla riippuen siitä, tarkastellaanko tasoaaltoimpedanssia vai piiri-impedanssia. Johtojen tai piirilevyn jälkien osalta käytämme:
Kulmataajuus:
ω = 2πf.
Induktiivinen reaktanssi:
X_L = 2πfL.
Kapasitiivinen reaktanssi:
X_C = 1 / (2πfC).
Impedanssi:
Z = R + jX_L + 1/(jX_C) = R + jωL + 1/(jωC).
Kun komponentilla on tunnettu resistanssi ja induktanssi, esimerkiksi ferriittihelmi, vastus, kondensaattori tai laitteet, joissa on loistehoja, on otettava huomioon, että impedanssi muuttuu taajuuden mukaan.
2.3 Nykyinen reitinvalintamekanismi
Yli joidenkin khz:n taajuusalueiden yläpuolella reaktanssi on yleensä suurempi kuin R. Mutta ei aina. Virta valitsee pienimmän impedanssin reitin. Joidenkin kHz:n alapuolella resistanssi voi olla pienin polku. Joidenkin khz:n yläpuolella reaktanssi voi hallita. Monet piirit toimivat yli kHz:n taajuudella, joten yksinkertainen ajatus “virta valitsee pienimmän resistanssin polun” ei enää täysin selitä, miten virta kulkee siirtojohdossa.
Yli 10 kHz:n virtaa kuljettavissa johtimissa virta valitsee reitin, jonka impedanssi on pienin. Jos kuorman impedanssi kytkeytyy johtimeen, kaapeliin tai jälkiin ja on suurempi kuin siirtotien rinnakkaiskapasitanssi, induktanssi hallitsee. Jos kaikilla kytketyillä johdoilla on samanlainen poikkileikkaus, pienimmän silmukkapinta-alan omaavalla reitillä on pienin induktanssi. Mitä pienempi silmukan pinta-ala on, sitä pienempi on induktanssi. Virta kulkee siis sitä kautta.
2.4 Jälki-induktanssin vaikutus RF-energiaan
Jokaisella johtimella on äärellinen impedanssi. Jälki-induktanssi on ainoa syy, miksi RF-energia voi esiintyä piirilevyllä. Myös pitkät sidosjohdot piisirun ja kiinnitysalustan välillä voivat aiheuttaa RF-energiaa. Levyn reititys voi aiheuttaa suuren induktanssin, varsinkin kun jäljet ovat pitkiä. Pitkä jälki tarkoittaa, että edestakainen pituus on pitkä. Tämä aiheuttaa jäljen aikaviiveen. Yksi signaali voi käynnistyä ennen kuin aikaisempi signaali palaa. Taajuusalueella jäljestä tulee “pitkä”, kun sen kokonaispituus on suurempi kuin noin λ/10 jäljessä esiintyvällä taajuudella.
Lyhyesti sanottuna: RF-jännite impedanssin yli muodostaa RF-virran. Tämä RF-virta voi säteillä energiaa vapaaseen tilaan ja rikkoa EMC-rajoja. Näissä esimerkeissä Maxwellin yhtälöt yhdistetään piirilevyjen reititykseen yksinkertaisella matematiikalla.
2.5 Magneettivuon suunnan oikean käden sääntö
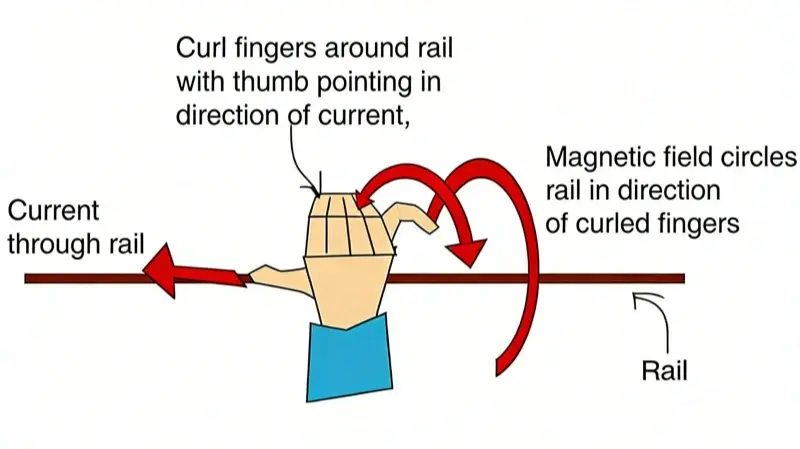
Maxwell sanoo, että jälkiä pitkin liikkuva varaus aiheuttaa virtaa. Virta synnyttää magneettikentän. Nämä magneettivuoroviivat seuraavat jälkeä. Käytä oikean käden sääntöä vuon suunnan löytämiseksi. Osoita peukalolla virran suuntaa. Käpristyneet sormesi osoittavat magneettikentän jäljen ympärillä. Ajassa muuttuva magneettikenttä aiheuttaa kohtisuoran sähkökentän. RF-säteily on tämän magneetti- ja sähkökentän sekoitus. Kentät voivat poistua piirilevystä säteilemällä tai johtumalla kytkettyjä kaapeleita pitkin.
Huomaa, että magneettikenttä kiertää suljetun silmukan rajaa. Piirilevyllä lähde ohjaa RF-virtaa lähteestä kuormaan jäljen kautta. RF-virran on palattava takaisin lähteeseen (Amperen laki). Tämä muodostaa RF-virtasilmukan. Silmukan ei tarvitse olla ympyränmuotoinen, mutta usein se on kierre. Koska paluupolku muodostaa suljetun silmukan, se muodostaa magneettikentän. Magneettikenttä synnyttää sähkökentän. Lähikentässä magneettiset osat voivat olla hallitsevia. Kaukokentässä suhde E/H (aaltoimpedanssi) on kuitenkin noin 120π Ω tai 377 Ω. Tämä arvo ei riipu lähteestä. Kaukokentässä voidaan siis käyttää silmukka-antennia ja herkkää vastaanotinta magneettisen osan mittaamiseen. Vastaanotettu virta on E/(120π) A/m, jos E on V/m. Myös sähköinen osa voidaan mitata sopivilla välineillä lähikentässä.
2.6 Suljetun piirin merkitys
Toinen yksinkertainen kuva RF:stä piirilevyillä saadaan kuvissa esitetyistä tyypillisistä piireistä. Käytä aika- ja taajuusalueanalyysiä. Kirchhoffin ja Amperen lakien mukaan piirin on oltava suljettu silmukka, jotta se toimisi. Kirchhoffin jännitelain mukaan jännitteiden summa minkä tahansa suljetun polun ympärillä on nolla. Ampereen lain mukaan virta aiheuttaa magneettista induktiota pisteessä, joka perustuu virtaan ja geometriaan.
Jos suljettua silmukkaa ei olisi, signaali ei voisi kulkea lähteestä kuormaan siirtojohdossa. Kun kytkin sulkeutuu, virtapiiri muodostuu ja vaihto- tai tasavirta virtaa. Taajuusalueella tämä virta on RF-energiaa. Aika- tai taajuusalueella ei ole erillistä virtaa. Yksi virta on olemassa, ja voimme nähdä sen kummallakin alueella. RF-paluureitin on oltava olemassa kuormasta lähteeseen, muuten piiri ei voi toimia. Siksi piirilevyrakenteen on noudatettava Maxwellin, Kirchhoffin ja Amperen periaatteita.
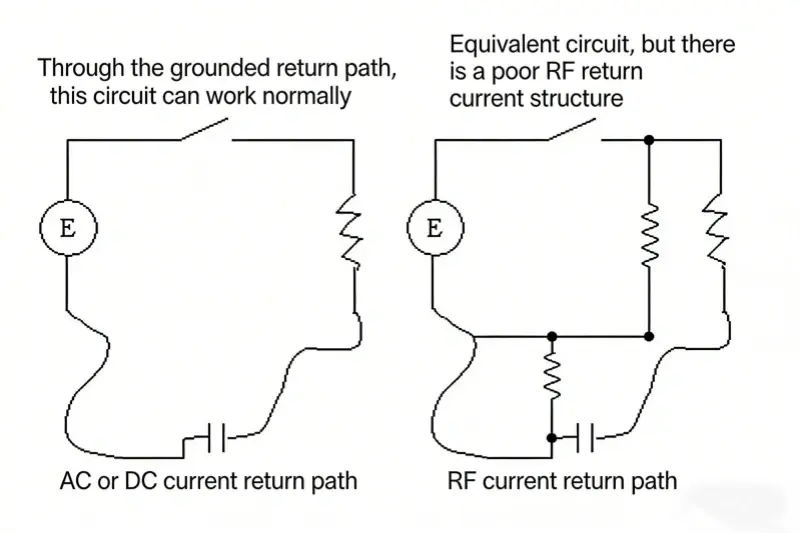
Kaikki nämä lait sanovat: jotta virtapiiri toimisi odotetulla tavalla, on oltava suljetun silmukan verkko. Kuvassa esitetään tällainen tyypillinen virtapiiri. Kun jälki kulkee lähteestä kuormaan, sen paluuvirtapolun on oltava olemassa. Se on Kirchhoff ja Ampere.

Toisessa kuvassa on kytkin ja ohjain E sarjassa. Kun kytkin on kiinni, piiri toimii. Jos se on auki, se ei toimi. Aika-alueella haluttu signaali kulkee lähteestä kuormaan. Signaalilla on oltava paluupolku, yleensä 0 V:n maadoitusreferenssin kautta. RF-virrat kulkevat lähteestä kuormaan ja palaavat pienimmän impedanssin polun kautta. Usein tämä tapahtuu maajäljen tai -tason, peilitason, kautta. Selitä RF-virta Amperen lain avulla.
3. Vuon minimointi (magneettivuon minimointi)
3.1 Magneettivuon syntymekanismi
Ennen kuin tutkimme “miten EMI näkyy piirilevyssä”, meidän on opittava, miten magneettijohdot muodostuvat siirtojohdoissa. Magneettivuo on keskeinen ajatus. Vuo muodostuu, kun virta kulkee kiinteän tai muuttuvan impedanssin läpi. Impedanssia on muun muassa johtimissa, komponenttien johtimissa ja läpivienneissä. Jos piirilevyllä on vuo, Maxwellin mukaan myös RF-energiareittejä on olemassa. Nämä polut voivat säteillä vapaaseen tilaan tai johtaa pois kaapeleiden kautta.
3.2 Virran kumoamisen periaate
RF-virran poistamiseksi piirilevystä käytämme “vuon kumoamista” tai “vuon minimointia”. Magneettijohdot kulkevat yhteen suuntaan jäljen ympäri. Jos RF-palautusreitti on samansuuntainen ja lähellä lähdeviivaa, paluupolun kenttä kulkee vastakkain lähdekentän kanssa. Kun kentät kulkevat vastakkaisiin suuntiin, ne kumoavat. Jos ei-toivottu vuo lähteen ja paluureitin välillä mitätöidään tai pidetään pienenä, säteilyä tai johdettua RF-virtaa ei esiinny, paitsi hyvin pienillä jäljen reunoilla. Vuon kumoamisen käsite on yksinkertainen. Suunnittelussa on kuitenkin varottava ansoja ja pieniä virheitä. Pieni virhe voi aiheuttaa monia ylimääräisiä ongelmia, jotka tekevät virheenkorjauksesta vaikeaa.
Helpoin vuon kumoamismenetelmä on käyttää kuvatasoa (peilitasoa). Riippumatta siitä, kuinka hyvin reitität, sähkö- ja magneettikenttiä on aina olemassa. Mutta jos peruutat magneettiset linjat, sähkömagneettinen häiriö katoaa. Se on niin yksinkertaista.
3.3 Vuon minimointi vinkkejä PCB Layoutissa
Kuinka peruuttaa vuo PCB-asettelussa? On monia vinkkejä. Kaikki eivät suoraan kumoa vuota. Joitakin yleisiä:
- Käytä monikerroksisia levyjä, joissa on oikea pinoamisjärjestys ja impedanssin säätö.
- Reititä kellojäljet lähelle paluumaatason (monikerroksisissa piirilevyissä). Käytä yksi- tai kaksipuolisissa levyissä maadoitusjälkiä tai suojapiirejä kellojälkien lähellä.
- Sieppaa magneettivuo muovipakkausten sisältä 0V-vertailuun komponenttien säteilyn vähentämiseksi.
- Valitse logiikkaosat huolellisesti, jotta voit vähentää osien säteilemää RF-spektriä. Käytä mahdollisuuksien mukaan laitteita, joissa on hitaampi reunanopeus.
- Vähennä kelloajureiden (TTL/CMOS) RF-ajojännitettä johtimien RF-virran pienentämiseksi.
- Pienempi maahäiriöjännite, joka esiintyy teho- ja maatasojen välillä.
- Kun monet laitteen nastat kytkeytyvät kerralla suuren kapasitiivisen kuorman ohjaamiseksi, huolehdi osan riittävästä irrotuksesta.
- Päätä kello- ja signaalijohdot asianmukaisesti, jotta vältetään soiminen, yli- ja aliohjaus.
- Käytä datajohtosuodattimia ja yhteismuotoisia kuristimia niitä tarvitsevissa verkoissa.
- Käytä ulkoisissa I/O-kaapeleissa ohituskondensaattoreita oikein (ei kytkentäerottimina).
- Jos komponentit säteilevät paljon yhteismuotoista RF-energiaa, anna niille maadoitettu jäähdytyselementti.
3.4 Muut sähkömagneettisen häiriön syyt piirilevyissä
Luettelon tarkastelu osoittaa, että magneettivuo on vain yksi osa piirilevyjen sähkömagneettista häiriötä. Muita syitä ovat mm:
- Piirin ja I/O-kaapeleiden väliset yhteismuoto- ja differentiaalimuotovirrat.
- Maasilmukat, jotka luovat magneettikenttärakenteita.
- Säteilyä aiheuttavat komponentit.
- Impedanssin epäsuhta.
Huomautus: suurin osa EMI-säteilystä on peräisin yhteismuotoisista jännitteistä. Levyllä tai piirissä nämä yhteismuototasot voivat muuttua pieniksi kentiksi.
Päätelmä
Jos haluat poistaa sähkömagneettisen häiriön piirilevyiltä, aloita vähentämällä magneettivuota. Sen sanominen on helppoa, mutta sen tekeminen on vaikeampaa. RF-energia on näkymätöntä ja sitä on vaikea löytää. Paikantamalla, missä RF-virta kulkee ja mihin suuntaan se kulkee, ja käyttämällä edellä mainittuja vinkkejä sekä Maxwellin, Kirchhoffin ja Amperen sääntöjä voit rajata epäilyttävän alueen. Etsi sitten todellinen EMI-lähde ja poista se.




